てこの原理 　支点を挟んで一方の腕には距離ｍの位置に重さＭのおもり、もう一方の腕には距離ｎの位置に重さＮのおもりが吊るされて釣り合っているとき、 　　　ｍ×Ｍ＝ｎ×Ｎ の関係が成り立つ。

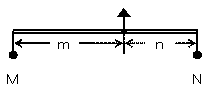
２．証明の方向

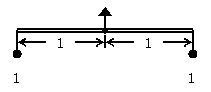
まず、ｍ＝ｎの場合、Ｍ＝Ｎとなることは対称性から自明とする。簡単のために、このとき、ｍ＝ｎ＝１、Ｍ＝Ｎ＝１と書く。長さおよび重さの単位は自由だから、こうしても一般性が保たれる。 　このてこを「てこ１／１」と言おう。１／１は左右の腕の長さを表す。
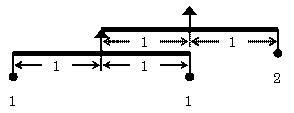
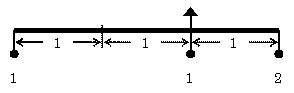
てこ１／１→てこ２／１ 　次に、上のてこ１／１をおもりをつけたまま、別のてこ１／１の一方の端に吊るす。上のてこのおもりの重さは合計で２であるから、新たなてこの他端には重さ２のおもりを吊るせばつり合う。 　新しいてこの端にある元のてこの支点を吊るす紐を短くして元のてこの腕と新たなてこの腕とが重なるようにする。 新たなてこの支点の真下にあるおもりは、釣り合いに関係ないからこれを除去しても釣り合いには影響しない。 　結局、腕の長さが１：２のてこ（てこ１／２）の場合には、両端に吊るすおもりを１：２としたとき釣り合うことが導けた。 　つまり、ｍ：ｎ＝１：２のとき、Ｍ：Ｎ＝２：１であるから、 　　　ｍ×Ｍ＝ｎ×Ｎ が成立する。
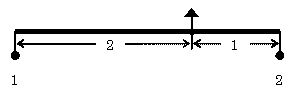
てこ１／１→てこ１／２ 　今は、もとのてこを新たなてこの左端に吊るしたが、逆に右端に吊るせば、てこ１／２の場合が導ける。
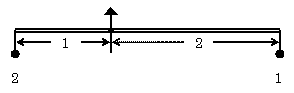
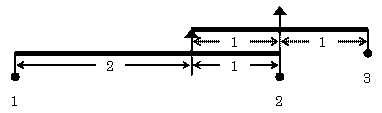
てこ２／１→てこ３／１ 　次は、てこ２／１を新たなてこ１／１の左端に吊るす。てこ２／１のおもりの合計が３であるから、新たなてこの右端には重さ３のおもりを吊るして釣り合いを保つ。 　前と同じように、元のてこの支点を支える紐の長さを0にし、2つの腕を重ねる。 　そして、支点の真下のおもりを除去する。 　こうして、腕の長さが３：１の場合には、おもりの比が１：３として釣り合うことが導かれる。 　つまりこの場合も、 　　　ｍ×Ｍ＝ｎ×Ｎ が成立する。
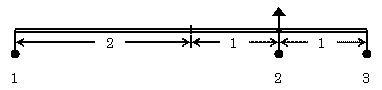
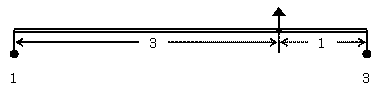
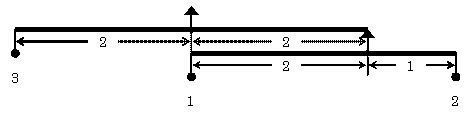
てこ２／１→てこ２／３ 　今とは逆に、てこ２／１を新たなてこの右端に吊るそう。この場合には、新たなてこは腕の長さが左右とも２のものを使う。なぜかと言うと、元のてこのおもりの片方が新たなてこの支点の真下に来ることが重要なのである。 　今までと同じように、もとのてこの支点を吊るす紐の長さを0にして、新たなてこの支点の真下のおもりを除去する。 　こうして、腕の長さが２：３の場合には、おもりの比が３：２として釣り合うことが導かれる。 　つまりこの場合も、 　　　ｍ×Ｍ＝ｎ×Ｎ が成立する。

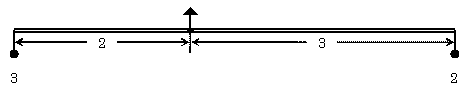
　　このようにして、てこｍ／ｎ（ｍ、ｎは正の整数）を次々と生成していくことができる。
　

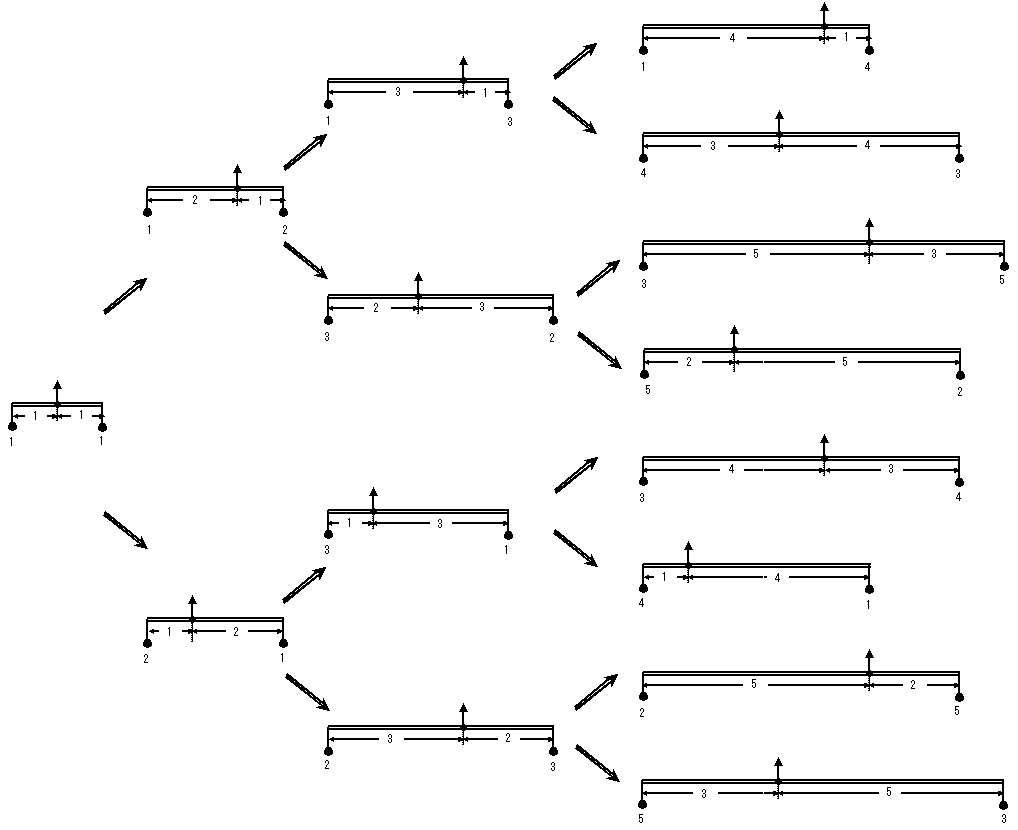
もう少し簡略化して、