
[�X�^�[�g�y�[�W]/[�ڎ��̃y�[�W]
�|�@���ɗ��W���_����@�|
���̂P
1997�N5��14��
�P�D���ɗ��W���_�Ƃ�
�@�@���ʁA�W���_�Ƃ����ΏW���ƏW���̕�܊W��������_��ł��B
�@�@�������A�����ł͕��ނ̓���Ƃ��Ď�舵���܂��B
���̈Ӗ��ł́A��W����łȂ��Ģ����(���͕���)��A��_��ł͂Ȃ��Ģ�p��ł��B
�@�@���̓����́A��܊W��\���L���@��,��,��,�� ���g�킸�A
�S�ē����@���i�y�т���Ɠ����Ȗ��@��,���j�ŕ\���Ă��邱�Ƃł��B
�Z�p���œ���݂́u�{�v(���@),�u�E�v(��@)�̂悤�ȋL�������g�킸�A�v�Z���w�ǎZ�p���Ɠ����ł��B
����ł��āA���낢��ȈӖ��Ŗ��ɗ��̂ł��B
�悸�A�u���̂P�v�ł́A��{�I�ȗp��Ƒ�����Љ�܂��B
�i�P�j�ړI�@
�@�@�W���Ƃ́A�����`���ꂽ�����̏W�܂�ł��B
�܂��A�P�P�̎����̂��Ƃ��W���̗v�f�Ƃ����܂��B
�����Ă����̗v�f�������ŕ����ĐV���ȏW�����`���܂��B
���낢��Ȋ��݂��邱�Ƃɂ�蕡�G�ɕ��ނ��ꂽ�W������`�ł��܂����A
����𐔊w�I�ɁA�Ƃ������Ƃ͒�^�I�Ɉ������Ƃ����̂��A���̏W���_�̖ړI�ł��B
�i�Q�j�S�̏W��
�@�@�������̎������������Ƃ���Ƃ��ɁA�悸���͈̔͂�ݒ肵�܂��B
�Ⴆ�������ɋ���S�O�l�̐��k�ł��B���̂S�O�l�������ŕ��ނ��邱�Ƃɂ��܂��B
���̗l�Ȏ��A���k�S�O�l�Ƃ����W�܂��S�̏W���Ƃ����܂��B
�S�̂�����Ƃ����Č����ĉF���S�̂ƍl���Ȃ��ʼn������B
�@�@����������ł� �h �Ə������Ƃɂ��܂��傤�B
�@�@�@�h���o�����ɋ���S�O�l�̐��k�p
�i�R�j��W��
�@�@�S�O�l�̐��k�������ŕ��ނ��܂��B
�Ⴆ�Βʊw�ɓd�Ԃ��g���Ă��邩�ۂ��ł��B
�d�Ԃ��g���Ă��鐶�k�̏W�܂���A���`�Ƃ��܂��傤�B
�@�@�@�`���o�d�Ԃ��g�����k�p
�@�@����Ǝc��̐��k�͓d�Ԃ��g���Ă��Ȃ��Ƃ������ƂɂȂ�܂��B
������W���`�̕�W���Ƃ����A�`^�Ə����܂��B
�@�@�@�`^���o�d�Ԃ��g��Ȃ����k�p
�i�S�j�݂��ɑf
�@�@�������̏W�������グ���Ƃ��A�����̏W���Ԃŋ��ʂ̗v�f���S���Ȃ��ꍇ�A
�����̏W���݂͌��ɑf�ł���Ƃ����܂��B
�Ⴆ�`�Ƃ`^�Ƃ݂͌��ɑf�ƂȂ�܂��B
�i�T�j�W���̘a
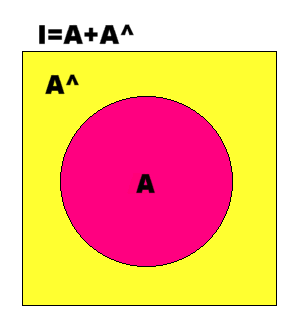 �@�@�Q�̏W���̗v�f�����킹�ĂP�̑傫�ȏW������邱�Ƃ��ł��܂��B
���̗l�ȑ���i�y�т��̌��ʁj��a�Ƃ����܂��B
�W���̘a�́@���@���́@�{�@�̋L���ŕ\���܂��B
�Ⴆ�A�`�Ƃ`^�̘a�͑S�̏W�� �h �ƂȂ�܂��B
�@�@�Q�̏W���̗v�f�����킹�ĂP�̑傫�ȏW������邱�Ƃ��ł��܂��B
���̗l�ȑ���i�y�т��̌��ʁj��a�Ƃ����܂��B
�W���̘a�́@���@���́@�{�@�̋L���ŕ\���܂��B
�Ⴆ�A�`�Ƃ`^�̘a�͑S�̏W�� �h �ƂȂ�܂��B
�@�@�@�h���`�{�`^
�@�@���āA�����œ����i���j�̈Ӗ���
�����̍����̏W���̗v�f�ƉE���̏W���̗v�f�Ƃ�
�S�Ĉ�v���Ă��邱�Ƃ�\���܂��B
�i�U�j�����ƍ���
�@�@����W�����݂��ɑf�ł��镡���̏W���ɕ����鑀����Ƃ����܂��B
�`�Ƃ`^�݂͌��ɑf�ŁA���̘a�� �h �ƂȂ�܂�����A�h �͂`�Ƃ`^�ɕ����o���邱�ƂɂȂ�܂��B
���̂��Ƃ���i���j�ŕ\���܂��B
�@�@�@�h ���`�{�`^�@�@���́@�@�`�{�`^�� �h
�@�@�����̋t�������Ƃ����܂��B
�@�@�@�`�{�`^�� �h�@�@���́@�@�h ���`�{�`^
�i�V�j�W���̐�
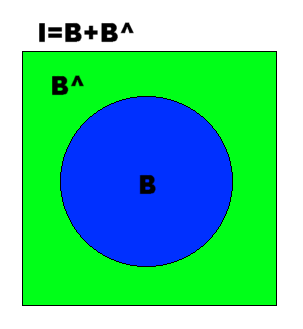 �@�@�����܂Œʊw�ɓd�Ԃ��g�����ۂ������ŕ����Ă��܂������A
���Ƀo�X���g�����ۂ��ŕ����Ă݂܂��傤�B
�ʊw�Ƀo�X���g���Ă��鐶�k�̏W�܂���a�Ƃ��܂��B
�@�@�����܂Œʊw�ɓd�Ԃ��g�����ۂ������ŕ����Ă��܂������A
���Ƀo�X���g�����ۂ��ŕ����Ă݂܂��傤�B
�ʊw�Ƀo�X���g���Ă��鐶�k�̏W�܂���a�Ƃ��܂��B
�@�@�@�a���o�o�X���g�����k�p
�@�@���̕�W���́A
�@�@�@�a^���o�o�X���g��Ȃ����k�p
�ƂȂ�܂��B���̂Ƃ���͂�A
�@�@�@�h���a�{�a^
�����藧���܂��B
�@�@���āA�ʊw�ɓd�Ԃƃo�X�̗����𗘗p���鐶�k�̏W�܂���A
�W���`�ƏW���a�̐ςƂ����A
�@�@�@�`���a�A�`�E�a�A���́@�`�a
�ŕ\���܂��B
�@�@�@�`�a���o�d�Ԃƃo�X�̗������g�����k�p
���l�ɁA�`�a^�A�`^�a�A�`^�a^�@�����̂悤�ɒ�`�ł��܂��B
�@�@�@�`�a^���o�d�Ԃ͎g�����A�o�X�͎g��Ȃ����k�p
�@�@�@�`^�a���o�d�Ԃ͎g��Ȃ����A�o�X�͎g�����k�p
�@�@�@�`^�a^���o�d�Ԃ��o�X���g��Ȃ����k�p
���̂Ƃ��A�`�a�A�`�a^�A�`^�a�A�`^�a^�݂͌��ɑf�ŁA����
�@�@�@�h���`�a�{�`�a^�{�`^�a�{�`^�a^
�����藧���܂��B
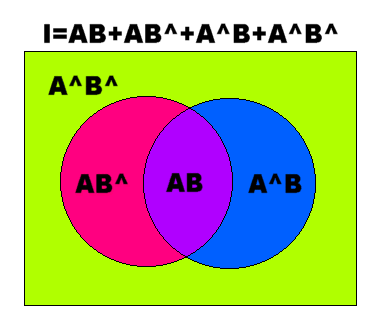
�i�W�j�f�W��
�@�@�`�a�A�`�a^�A�`^�a�A�`^�a^��f�W���Ƃ����܂��B
���m�ɂ́A�W���`�ƏW���a�i�ɑΉ����閽��[�`]�Ɩ���[�a]�j
�Ɋւ���f�W���ƌ����܂��B
���l�ɁA�W���`�Ɋւ���f�W���͂`�Ƃ`^�ł���A
�W���a�Ɋւ���f�W���͂a�Ƃa^�ƂȂ�܂��B
�i�X�j�W�J
�@�@���ނƂ́A�S�̏W����f�W���̘a�̌`�ɕ������邱�Ƃł��B
[�`]�Ƃ�����ł̕��ނ́A
�@�@�@�h���`�{�`^�@�@�@�@�@�@�@�@�@�@�@�@�@�@�c�@
[�a]�Ƃ�����ł̕��ނ́A
�@�@�@�h���a�{�a^�@�@�@�@�@�@�@�@�@�@�@�@�@�@�c�A
[�`�C�a]�Ƃ�����ł̕��ނ́A
�@�@�@�h���`�a�{�`�a^�{�`^�a�{�`^�a^ �@ �@�c�B
�ł��B�B�̎��́A�@�y�чA���玟�̂悤�ɓ������Ƃ��ł��܂��B
�@�@�@�h���h�E�h���i�`�{�`^�j�i�a�{�a^�j���`�a�{�`�a^�{�`^�a�{�`^�a^
�����[�b]�Ƃ������������A
�@�@�@�h���b�{�b^
�ł�����A
[�`�C�a�C�b]�Ƃ�����ł̕��ނ́A
�h���h�E�h�E�h���i�`�{�`^�j�i�a�{�a^�j�i�b�{�b^�j
�@���`�a�b�{�`�a�b^�{�`�a^�b�{�`�a^�b^�{�`^�a�b�{�`^�a�b^�{�`^�a^�b�{�`^�a^�b^
�ƂȂ�܂��B
���̂Q�@�ɂÂ�
[�X�^�[�g�y�[�W]/[�ڎ��̃y�[�W]


 �@�@�Q�̏W���̗v�f�����킹�ĂP�̑傫�ȏW������邱�Ƃ��ł��܂��B
���̗l�ȑ���i�y�т��̌��ʁj��a�Ƃ����܂��B
�W���̘a�́@���@���́@�{�@�̋L���ŕ\���܂��B
�Ⴆ�A�`�Ƃ`^�̘a�͑S�̏W�� �h �ƂȂ�܂��B
�@�@�Q�̏W���̗v�f�����킹�ĂP�̑傫�ȏW������邱�Ƃ��ł��܂��B
���̗l�ȑ���i�y�т��̌��ʁj��a�Ƃ����܂��B
�W���̘a�́@���@���́@�{�@�̋L���ŕ\���܂��B
�Ⴆ�A�`�Ƃ`^�̘a�͑S�̏W�� �h �ƂȂ�܂��B �@�@�����܂Œʊw�ɓd�Ԃ��g�����ۂ������ŕ����Ă��܂������A
���Ƀo�X���g�����ۂ��ŕ����Ă݂܂��傤�B
�ʊw�Ƀo�X���g���Ă��鐶�k�̏W�܂���a�Ƃ��܂��B
�@�@�����܂Œʊw�ɓd�Ԃ��g�����ۂ������ŕ����Ă��܂������A
���Ƀo�X���g�����ۂ��ŕ����Ă݂܂��傤�B
�ʊw�Ƀo�X���g���Ă��鐶�k�̏W�܂���a�Ƃ��܂��B
