
[スタートページ]/[目次のページ]
− 役に立つ集合論入門 −
その2
1997年5月14日
2.役に立つとは
その1で、素集合という考え方を紹介しました。
この考え方を使うといかに便利かをその2で説明します。
(1)普通言語との対応が素直
例えば、集合の和 A∪B を普通の言葉で表現すると、
「集合Aと集合Bのいずれか一方もしくは両方に属する要素の集まり」
となります。
この言い方を素直に集合の表現に置き換えると、
集合Aと集合Bのいずれか一方 → AB^+A^B
もしくは両方 → +AB
ですから、A∪Bよりも、AB^+A^B+AB と書く方が自然です。
(2)公式が簡単
任意の集合Aに対し、次のような殆ど自明な関係が成り立つ。
1)A・I=I・A=A (全体集合は数字の1に似ている)
2)A・A=A
3)A・A^=A^・A=0 (0は要素がないという意味の記号)
4)A+0=0+A=A
5)A+A^=A^+A=I
6)A+A=A
任意の集合AとBに対し、次の交換法則が成り立つ。
7)A+B=B+A
8)A・B=B・A
任意の集合A,B,Cに対し、次の結合法則及び分配法則が成り立つ。
9)(A+B)+C=A+(B+C)
10)(A・B)・C=A・(B・C)
11)A・(B+C)=A・B+A・C
但し、乗法(・)は加法(+)に優先します。
以上のような、非常に簡単な公式だけで十分ことが足ります。
いわゆる集合論にある公式
12)(A+B)^=A^・B^ (ド・モルガンの法則)
13)(A・B)^=A^+B^ (ド・モルガンの法則)
14)A+B・C=(A+B)・(A+C) (加法についての分配法則)
のような難しいものは不要です。
(3)要素の数も同じ公式
ある集合の要素の数を求める場合、その集合を素集合の和で表し、
おのおのの素集合の要素の数を式のとおりに足せば良いのです。
例えば、教室に40人の生徒がいた(I=40人)として、
通学に電車を使う生徒が15人いれば(A=15人)、
通学に電車を使わない生徒(A^)は
I(40人)=A(15人)+A^
から、40−15=25(人)と求められます。
さらに、通学にバスを使う生徒が25人おり(B=25人)、
通学に電車とバスの両方を使う生徒が10人いたとすれば(AB=10人)、
I=(A+A^)(B+B^)=AB+AB^+A^B+A^B^=40
A=AI=A(B+B^)=AB+AB^=15
B=IB=(A+A^)B=AB+A^B=25
AB=10
と式を立てることができます。
これは、AB,AB^,A^B,A^B^を未知数とする4元連立1次方程式です。
これを解くと、
AB=10,AB^=5,A^B=15,A^B^=10
が簡単に求まります。
これを普通の集合論でやりますと、例えば A∪B(=A+B)すなわち
電車とバスのいずれか一方もしくは両方を使う生徒の数を求める場合、
n(A∪B)=n(A)+n(B)−n(A∩B)
という公式を持ち出さなくてはなりません。
こんな公式を持ち出すくらいならベン図をそのまま使った方がずっとマシなわけですし、
通学に30分以上かかるか否かといった別の基準でさらに分類する場合には
「n(A∪B∪C)を求める公式はどんなだったろうか?」
と殆どお手上げです。
「役に立つ集合論」なら簡単です。
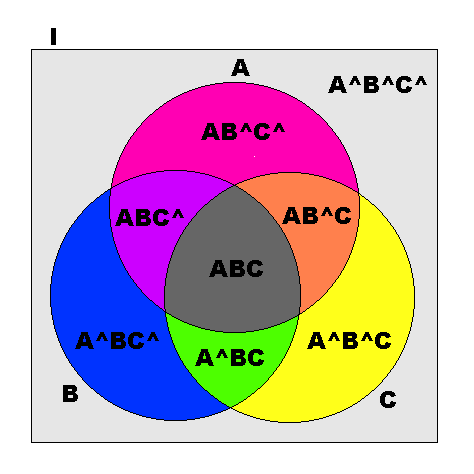
I=(A+A^)(B+B^)(C+C^)
=ABC+ABC^+AB^C+AB^C^+A^BC+A^BC^+A^B^C+A^B^C^
A=A(B+B^)(C+C^)=ABC+ABC^+ AB^C+AB^C^
B=(A+A^)B(C+C^)=ABC+ABC^+A^BC+A^BC^
C=(A+A^)(B+B^)C=ABC+AB^C+A^BC+A^B^C
A∪B=A+B=A(B+B^)(C+C^)+(A+A^)B(C+C^)
=ABC+ABC^+AB^C+AB^C^+A^BC+A^BC^
B∪C=B+C=(A+A^)B(C+C^)+(A+A^)(B+B^)C
=ABC+ABC^+AB^C+A^BC+A^BC^+A^B^C
A∪C=A+C=A(B+B^)(C+C^)+(A+A^)(B+B^)C
=ABC+ABC^+AB^C+AB^C^+A^BC+A^B^C
A∪B∪C=A+B+C
=A(B+B^)(C+C^)+(A+A^)B(C+C^)+(A+A^)(B+B^)C
=ABC+ABC^+AB^C+AB^C^+A^BC+A^BC^+A^B^C
=I−A^B^C^
など、お手のものです。
その3 につづく
[スタートページ]/[目次のページ]


