[スタートページ]/[目次のページ]

−　役に立つ集合論入門　−

その３
1997年5月24日

３．論理とブール代数
　　ここでは、特に説明しません。以下の真理表で、「１」が「真」に、「０」が「偽」にそれぞれ対応します。



[命題Ａに対して]
場合分け補集合適用例
ＡＡ^ＡＡ^Ａ＋Ａ^
1001
0101


[命題Ｂに対して]
場合分け補集合適用例
ＢＢ^ＢＢ^Ｂ＋Ｂ^
1001
0101


[命題Ａ，Ｂに対して]
場合分け補集合素集合適用例
ＡＢＡ^Ｂ^ＡＢＡＢ^Ａ^ＢＡ^Ｂ^Ａ+ＢＡＢ(Ａ+Ｂ)^(ＡＢ)^
1 1 0 0 1 0 0 0 1 1 0 0
1 0 0 1 0 1 0 0 1 0 0 1
0 1 1 0 0 0 1 0 1 0 0 1
0 0 1 1 0 0 0 1 0 0 1 1


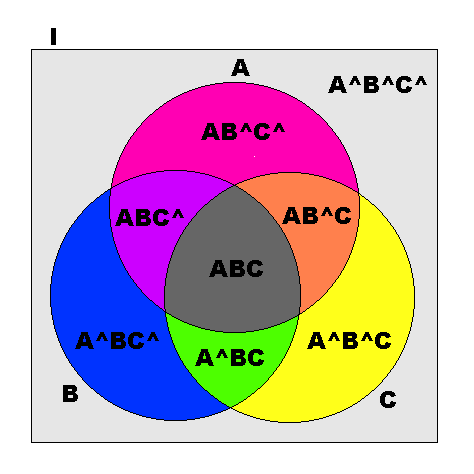
[命題Ａ，Ｂ，Ｃに対して]
場合分け補集合素集合適用例
ＡＢＣＡ^Ｂ^Ｃ^ＡＢＣＡＢＣ^ＡＢ^ＣＡＢ^Ｃ^Ａ^ＢＣＡ^ＢＣ^Ａ^Ｂ^ＣＡ^Ｂ^Ｃ^Ａ+Ｂ+Ｃ
1 1 1 0 0 0 1 0 0 0 0 0 0 0 1
1 1 0 0 0 1 0 1 0 0 0 0 0 0 1
1 0 1 0 1 0 0 0 1 0 0 0 0 0 1
1 0 0 0 1 1 0 0 0 1 0 0 0 0 1
0 1 1 1 0 0 0 0 0 0 1 0 0 0 1
0 1 0 1 0 1 0 0 0 0 0 1 0 0 1
0 0 1 1 1 0 0 0 0 0 0 0 1 0 1
0 0 0 1 1 1 0 0 0 0 0 0 0 1 0




その４　につづく
[役に立つ集合論（その２）に戻る] [役に立つ集合論（その４）へ行く]

[スタートページ]/[目次のページ]