
[スタートページ]/[目次のページ]
− 有理数の正しい数え方 −
その9
2002年11月4日
シュテルン=ブロコットの二分木と有理数の階層
有理数の正しい数えかた(その8)で示したシュテルン=ブロコット樹の太線だけを取り出したのが下の図である。
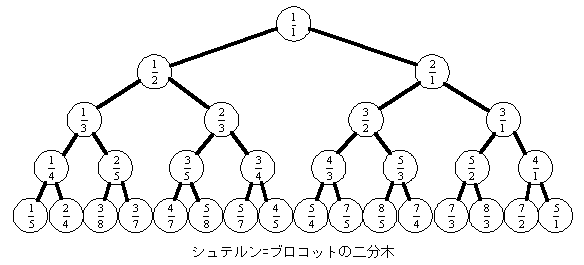
上に示したシュテルン=ブロコットの二分木は、完全二分木(上から下に向け必ず2つずつに分かれる)であり、二分探索木(右に行くほど大きい値を持つ)である。
次に別の二分木を示す。
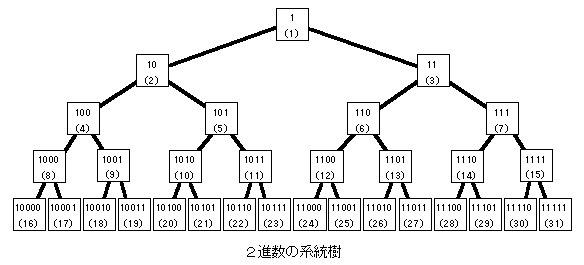
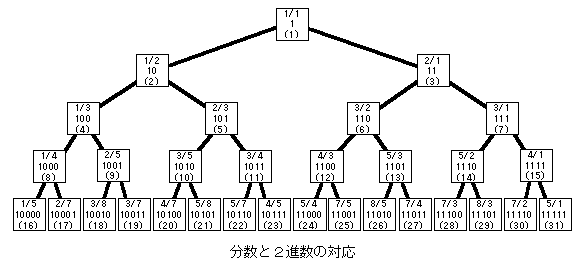
2進数の系統樹と命名したが、元素周期律表に倣って「2進数の周期律表」と名づけてもよい。どういう成り立ちになっているかは明白である。各ノード(数値が記載してある節点)から子(下にある2つのノード)を見るとき、左の子に移るときには最終桁に「0」を付加し、右の子に移るときには最終桁に「1」を付加する。括弧内には対応する10進数を示した。2進数の系統樹は、やはり完全二分木であり、逆ヒープ(下に行くほど大きい)である。さて、シュテルン=ブロコットの二分木は、有理数の正しい数え方(その4)で示した「有理数の階層」と全く同じである。また、シュテルン=ブロコットの二分木と2進数の系統樹とを重ね合わせて、分数(有理数)と2進数(自然数)を対応付けたものは、有理数の正しい数え方(その2)及び(その3)で示したものに完全に一致する。
[スタートページ]/[目次のページ]




