有理数の正しい数えかた(その3)で示した有理数と整数の対応関係をもとに、有理数から対応する整数を求めるアルゴリズム、逆に整数から対応する有理数を求めるアルゴリズムをフローチャートで示す。
　ほとんどが符号処理に費やされていて、実質的な計算は極くわずかである。

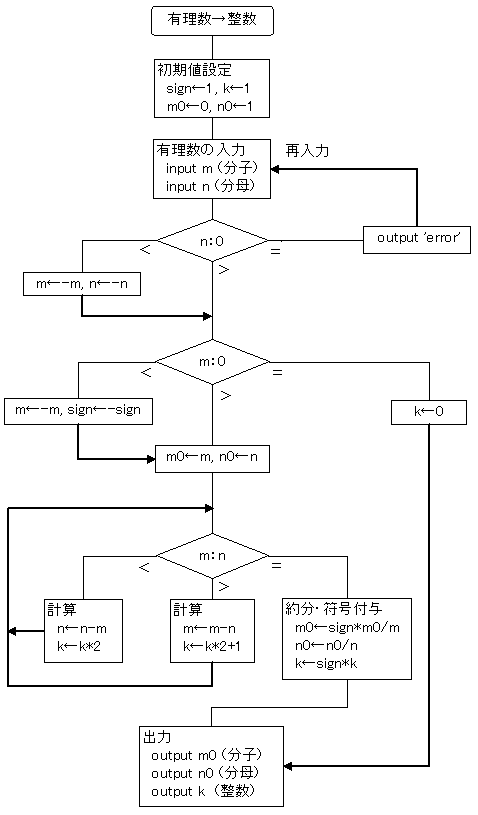
（１）有理数→整数
　任意の有理数を2つの整数：m(分子)，n(分母)で与えたとき、対応する整数 k を一意的に求める。
　m/n が既約分数でない場合にも対応するために、約分した既約分数 m0/n0 の分子(m0)と分母(n0)も併せて算出する。
　このとき、＋・−の符号は分子の側 m0 に一括する。
　たとえば、
　　　・ m=1, n=1 (1/1)　→　k=1, m0=1, n0=1 (1/1)
　　　・ m=-3, n=1 (-3/1)　→　k=-7, m0=-3, n0=1 (-3/1)
　　　・ m=7, n=-5 (7/-5)　→　k=-121, m0=-7, n0=5 (-7/5)
　　　・ m=-14, n=-10 (-14/-10)　→　k=121, m0=7, n0=5 (7/5)

 

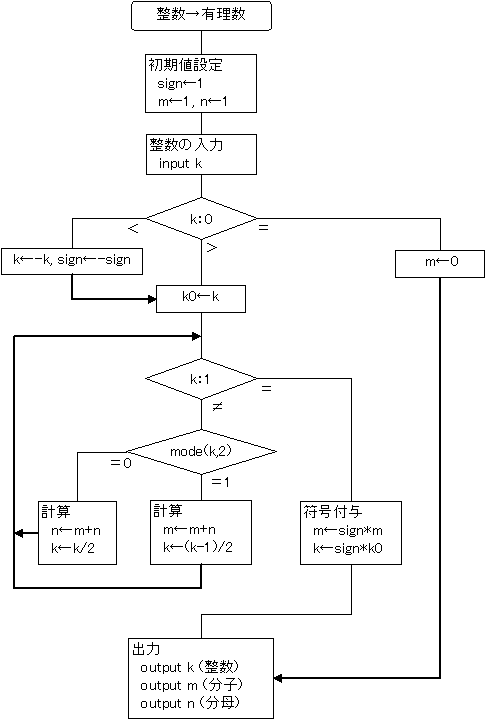
（２）整数→有理数
　任意の整数 k を与えたとき、これに対応する有理数を既約分数 m/n として一意的に求める。
　このとき、＋・−の符号は分子の側 m に一括する。
　たとえば、
　　　・ k=1　→　m=1, n=1 (1/1)
　　　・ k=-7　→　m=-3, n=1 (-3/1)
　　　・ k=-121　→　m=-7, n=5 (-7/5)
　　　・ k=121　→　m=7, n=5 (7/5)