「その10」では、有理数から対応する整数を求めるアルゴリズム、逆に整数から対応する有理数を求めるアルゴリズムをフローチャートで示した。
　ただし、そのアルゴリズムのほとんどが符号処理に費やされていて、実質的な計算は極くわずかであった。
　これは、経済的でないため、「その11」では、正値限定のアルゴリズムを示すことにした。
　　すなわち、有理数は分母･分子とも正の整数（つまり自然数）からなる既約分数とし、これと正の整数（つまり自然数）とを１対１に対応させる。
　　これを、0および負の有理数まで拡張するには、有理数0を整数0に対応させ、負の有理数をこれと絶対値が等しい正の有理数に対応する整数に負号を付けた整数に対応させればよい。実際、「その10」では、そのようになっている。

（１）有理数の一意的表現
　任意の有理数を2つの整数、m(分子)およびn(分母)の分数（比の値）として定義することができる。
　一般的な表現では、mは整数、nは0でない整数とする。また、n=1の場合は分母を省略し、分子のみを記述する。
　しかし、ここでは、mは整数、nは正の整数（つまり自然数）とし、mとnは互いに素とする。こうすれば、有理数は一意的に表現できる。
　
　たとえば、
　　　・ 有理数 0 は、0, -0, 0/1, 0/2, -0/(-3), ・・・などと書くことができるが、ここでは 0/1 を標準的な表現とする。
　　　・ 有理数 1 は、1, 1/1, 2/2, -2/(-2), 55/55, ・・・などと書くことができるが、 1/1 を標準とする。
　　　・ 有理数 1/3 は、1/3, 2/6, -3/(-9), ・・・などと書くことができるが、1/3 を標準とする。
　　　・ 有理数 -3/8 は、-3/8, 3/(-8), -6/16, 9/(-24), ・・・などと書くことができるが、 -3/8 を標準とする。
　　　・ 有理数 10 は、10, 10/1, -20/(-2), 50/5, などと書くことができるが、10/1 を標準とする。

　そして、正の有理数とは、分母(n)に加えて、分子(m)も正の整数(つまり自然数)であるということができる。
　つまり、有理数の正負は、分子(m)の正負で決まる。

（２）正の有理数　vs.　自然数　−−−対応のアルゴリズム
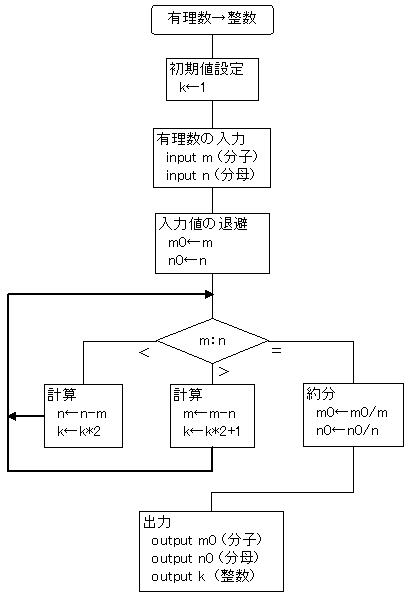
　任意の正の有理数 m/n (m, nは互いに素である自然数)を与えたとき、対応する自然数を一意的に求めるアルゴリズムを次のフローチャートで示す。

　

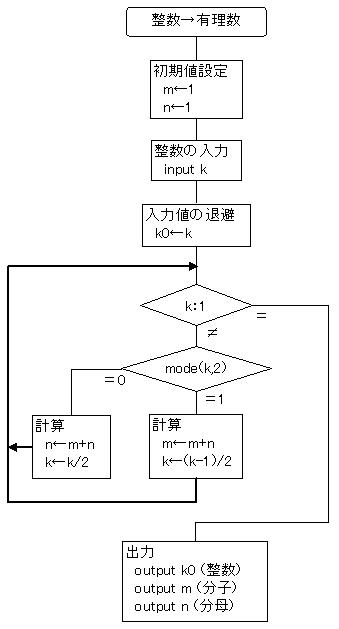
次に、任意の自然数 k を与えたとき、これに対応する正の有理数 m/n を既約分数としてとして一意的に求めるアルゴリズムを次のフローチャートで示す。